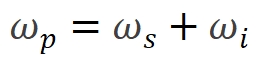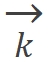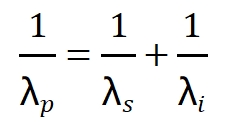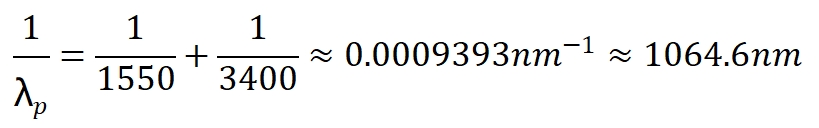科研计算器 | 光参量过程中的波长转换
2025.04.11
引言
在现代光学研究中,非线性光学效应扮演着越来越重要的角色。其中,光学参量放大(Optical Parametric Amplification, OPA)作为一种重要的频率转换技术,已广泛应用于激光技术、光谱分析和量子光学等领域。理解泵浦光、信号光和闲频光三者之间的波长关系,对于设计和优化光学参量放大器至关重要。本文将系统介绍这一关系的物理原理、数学表达及实际应用。
概念
光学参量放大器(OPA)
光学参量放大器是一种利用二阶非线性光学效应的器件,通过非线性晶体中的参量过程,将高强度的泵浦光能量转换为信号光和闲频光。这一过程需要满足严格的能量守恒和动量守恒条件。
三波相互作用
在OPA过程中涉及三种光波:
计算公式
能量守恒关系
波长关系式
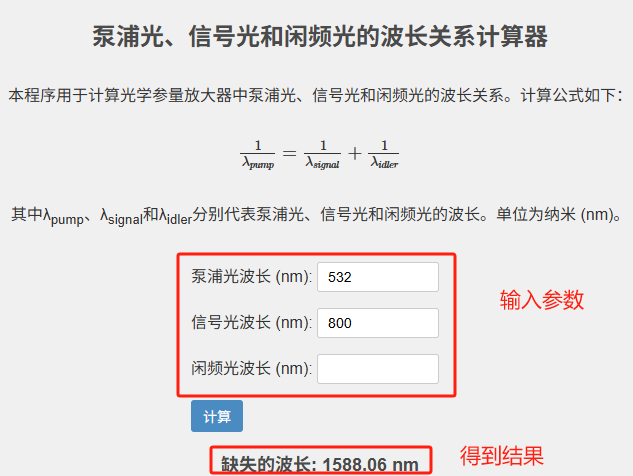
使用方法
计算器功能说明
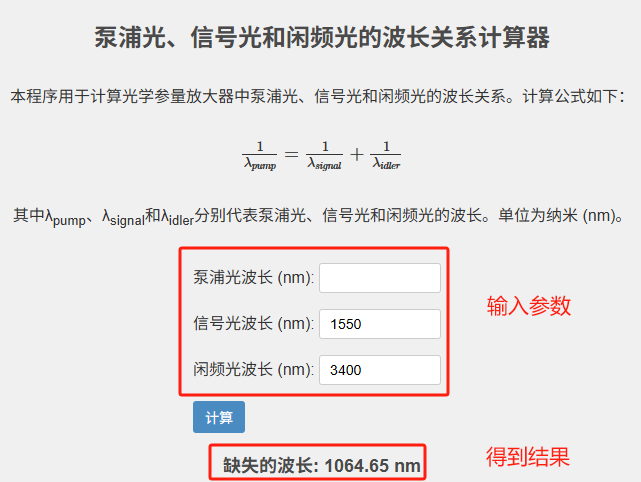
基于上述原理,我们可以建立一个实用的计算工具,用于确定OPA系统中未知的波长参数。计算规则如下:
已知任意两个波长,可求出第三个波长
操作步骤
1.在已知的两个玻璃厂输入框中填入数值(单位:nm)
2. 将待求波长对应的输入框留空或设为0
3. 执行计算操作
4.获取计算结果病应用于实验设计
实例解析
光学参量放大器波长关系计算实例
下面通过三个典型例子,详细展示如何代入公式计算光学参量放大器中缺失的波长参数。
根据能量守恒关系:

结语
光学参量放大器中三波长的关系计算是非线性光学研究和应用中的重要基础。通过本文介绍的能量守恒原理和相应计算公式,研究人员可以有效地设计和优化OPA系统。理解这些基本原理不仅有助于实验参数的确定,更能为新型光学器件的开发提供理论指导。随着激光技术的不断发展,光学参量放大技术在光谱分析、量子信息等领域的应用前景将更加广阔。掌握这些基础计算方法,将为相关领域的研究工作带来极大便利。
如您在计算器的使用过程中发现有任何问题或错误,请及时与我们联系,我们将及时修改,并且为感谢您的信任与监督,我们特意为您准备了一份“监督奖励”,如有其他需要我们补充添加的也欢迎联系我们,我们非常荣幸可以为各位的科研经历提供些许便利。
科研之路,道阻且长,预祝各位专家学者科研顺利,早出成果。
在现代光学研究中,非线性光学效应扮演着越来越重要的角色。其中,光学参量放大(Optical Parametric Amplification, OPA)作为一种重要的频率转换技术,已广泛应用于激光技术、光谱分析和量子光学等领域。理解泵浦光、信号光和闲频光三者之间的波长关系,对于设计和优化光学参量放大器至关重要。本文将系统介绍这一关系的物理原理、数学表达及实际应用。
概念
光学参量放大器(OPA)
光学参量放大器是一种利用二阶非线性光学效应的器件,通过非线性晶体中的参量过程,将高强度的泵浦光能量转换为信号光和闲频光。这一过程需要满足严格的能量守恒和动量守恒条件。
三波相互作用
在OPA过程中涉及三种光波:
- 泵浦光(ωₚ):提供能量的高强度激光
- 信号光(ωₛ):需要被放大的弱光信号
- 闲频光(ωᵢ):能量转换过程中伴生的光波
计算公式
能量守恒关系
OPA过程的基础是能量守恒原理,其数学表达式为: |
其中ℏ是约化普朗克常数。约去ℏ后得到频率关系:
|
波长关系式
|
由于光速c=λν=λω/2π,我们可以将频率关系转换为更实用的波长关系: 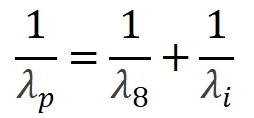 这一公式建立了三种光波波长之间的定量关系,是设计和分析OPA系统的关键方程。 |
动量守恒(相位匹配) 实际应用中还需满足动量守恒:
其中 |
使用方法
计算器功能说明
基于上述原理,我们可以建立一个实用的计算工具,用于确定OPA系统中未知的波长参数。计算规则如下:
已知任意两个波长,可求出第三个波长
|
当泵浦光波长未知时:
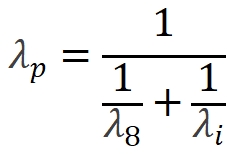 |
当信号光波长未知时:
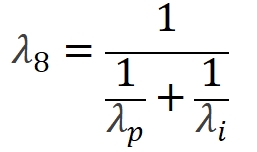 |
当闲频光波长未知时:
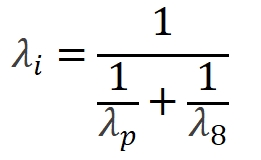 |
操作步骤
1.在已知的两个玻璃厂输入框中填入数值(单位:nm)
2. 将待求波长对应的输入框留空或设为0
3. 执行计算操作
4.获取计算结果病应用于实验设计
实例解析
光学参量放大器波长关系计算实例
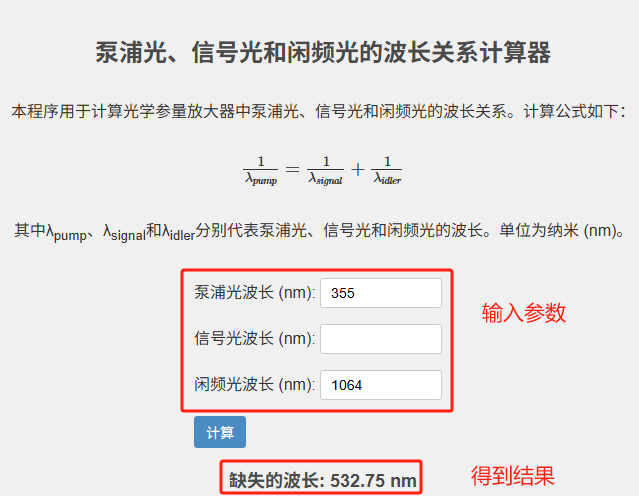
下面通过三个典型例子,详细展示如何代入公式计算光学参量放大器中缺失的波长参数。
根据能量守恒关系:

|
实例1:计算闲频光波长
已知条件:
推出闲频光计算公式代入数值:
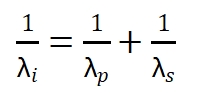  |
实例2:计算泵浦光波长
推出泵浦光计算公式代入数值: |
| 实例3:计算信号光波长 已知条件:
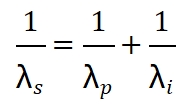  |
|
 |
|
 |
|
结语
光学参量放大器中三波长的关系计算是非线性光学研究和应用中的重要基础。通过本文介绍的能量守恒原理和相应计算公式,研究人员可以有效地设计和优化OPA系统。理解这些基本原理不仅有助于实验参数的确定,更能为新型光学器件的开发提供理论指导。随着激光技术的不断发展,光学参量放大技术在光谱分析、量子信息等领域的应用前景将更加广阔。掌握这些基础计算方法,将为相关领域的研究工作带来极大便利。
如您在计算器的使用过程中发现有任何问题或错误,请及时与我们联系,我们将及时修改,并且为感谢您的信任与监督,我们特意为您准备了一份“监督奖励”,如有其他需要我们补充添加的也欢迎联系我们,我们非常荣幸可以为各位的科研经历提供些许便利。
科研之路,道阻且长,预祝各位专家学者科研顺利,早出成果。

 智能助手
智能助手