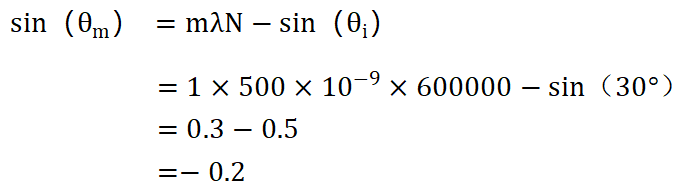引言:
在光学领域,反射光栅(Reflective Gratings)作为关键的光学元件,广泛应用于光谱分析、激光技术以及光通信系统中。精确理解反射光栅的工作原理及其核心参数,如衍射角(Diffracted Angle)和利特罗角(Littrow Angle),对于优化光学设计和提升系统性能具有重要意义。本文旨在系统阐述反射光栅的基本概念、相关计算公式及其实际应用,并通过具体示例说明其计算方法。
概念:
反射光栅是一种表面具有周期性结构的光学元件。当光线以一定角度入射到光栅表面时,由于光栅的微观结构,入射光会发生衍射,生成多个方向的衍射光。衍射光的分布和强度依赖于光栅的参数及入射光的性质。
衍射角指的是衍射光相对于入射光的偏转角度。在特定的衍射级次(Order, m)下,衍射光的角度θm可通过光栅方程计算得出。
利特罗角是一种特殊情况下的衍射角度,此时入射光与衍射光在同一平面内且方向相反,即衍射角等于入射角。利特罗角的存在使得光栅在该角度下的衍射效率达到最大,因而在高精度光谱分析中具有重要应用价值。
计算公式:
反射光栅的衍射角和利特罗角的计算基于以下公式:
|
衍射角公式: 其中: · N为光栅的光线密度,单位通常为每毫米的线数(1/mm)。 · m为衍射级次,可以为正或负整数。 · λ为入射光的波长,单位为纳米(nm)。 · θi为入射角,单位为度(°)。 · θm为衍射角,单位为度(°)。 通过该公式,可以解出衍射角θ: θm=arcsin(mλN-sin(θi)) |
利特罗角公式: |
使用方法:
1.输入参数:
· 光栅光线密度N(1/mm)
· 入射角θi(°)
· 衍射级次m
· 波长λ(nm)
2.单位转换:
· 将光栅密度N从1/mm转换为1/m。
· 将波长λ从纳米(nm)转换为米(m)。
· 将入射角θi从度转换为弧度。
3.计算衍射角θm:
· 使用衍射角公式计算sin(θm)。
· 通过反正弦函数得到θm的值(需确保sin(θm)的值在-1到1之间)。
4.计算利特罗角θ:
· 使用利特罗角公式计算sin(θ)。
· 通过反正弦函数得到θ的值(需确保sin(θ)的值在-1到1之间)。
5.输出结果:
· 衍射角θm(°)
· 利特罗角θ(°)
示例:
|
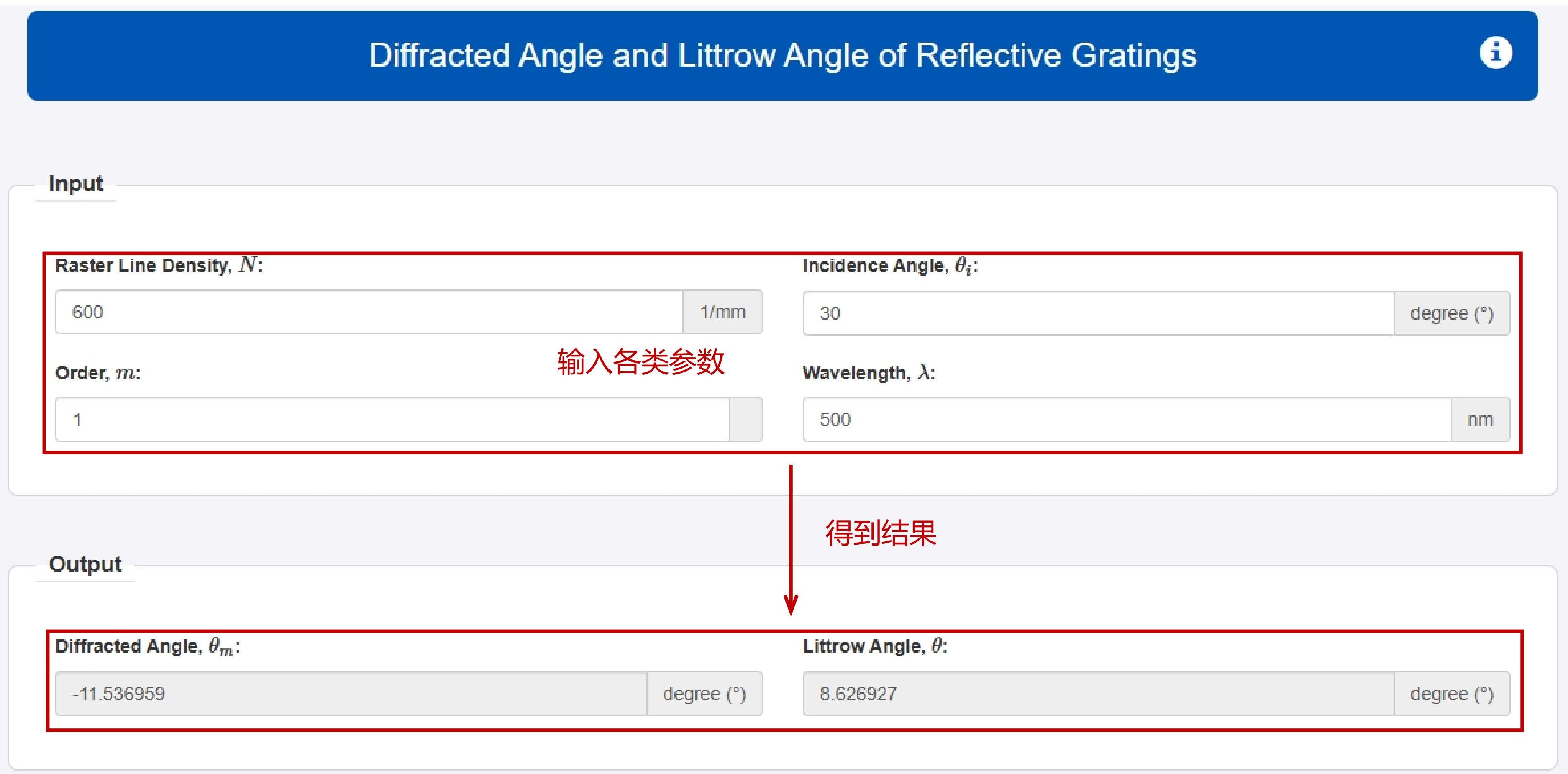
已知参数: · 光栅密度N=600线/mm · 入射角θi=30° · 衍射级次m=1 · 波长λ=500nm |
单位转换: N=600线/mmx1000=600000线/m λ=500nm=500x10-9m θi=30°x(π/180)=0.5236弧度 |
|
计算衍射角θm: |
计算利特罗角θ: 衍射角θm≈−11.54° 利特罗角θ≈8.63° |
点击图片,跳转网页
如您在计算器的使用过程中发现有任何问题或错误,请及时与我们联系,我们将及时修改,并且为感谢您的信任与监督,我们特意为您准备了一份“监督奖励”,如有其他需要我们补充添加的也欢迎联系我们,我们非常荣幸可以为各位的科研经历提供些许便利。科研之路,道阻且长,预祝各位专家学者科研顺利,早出成果。

 智能助手
智能助手